1．抵抗-温度特性

抵抗-温度特性とは、ゼロ負荷抵抗値と素子温度との関係をいいます。この抵抗-温度特性は実測によって求めます。しかし、B定数が明らかな場合は、ある温度範囲において近似的に次の式で求めることができます。

上記の式では、ゼロ負荷抵抗値の対数と絶対温度の逆数とが直線関係にあることを示します。
抵抗-温度特性例を図3.1.1に示します。

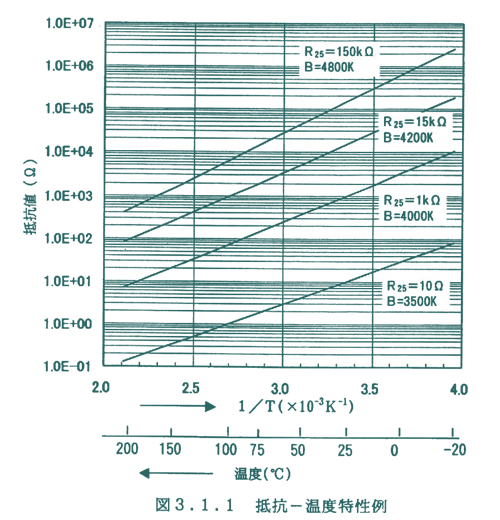
2．ゼロ負荷抵抗値

サーミスタは周囲温度を一定にして抵抗値を測定します。しかし、抵抗測定時の電流による自己発電の影響で、理論的に正確な抵抗値を測定することができないため、通常、自己発熱の無視できる状態で抵抗値の測定を行ないます。

ゼロ負荷抵抗値とは、測定の総合誤差に比べ、自己発熱による抵抗変化が無視できるような （熱放散定数の1/20以下の電力）十分低い消費電力（以下、"ゼロ負荷"という。）での、規定温度で測定したときのサーミスタ素子の直流抵抗値をいいます。

また、規格値を代表するゼロ負荷抵抗値を公称ゼロ負荷抵抗値と呼び、特に規定が無い限り、周囲温度25℃での値を公称ゼロ負荷抵抗値とします。公称ゼロ負荷抵抗値に対する推奨許容差は、表3.1.1.1に示すようにJIS　C 2570-1998 （直熱形NTCサーミスタ通）で次のように規定されています。従いまして同じ抵抗値公差もB定数の高い方が結果的に精度が優れていると言う事になります。

上記表の計算式は抵抗値許容差をゼロ負荷抵抗温度係数（αT）で割って求められています。実際に計算すると＋側、－側が同じになるはずですが、上記表は若干編集してあります。

公称ゼロ負荷抵抗値に対する許容差が小さいほど回路の設計はしやすくなりますが、許容差が小さいほど高価になるのでサーミスタの許容差をできるだけ広くとれるような回路設計をすることが望ましいといえます。

3．B定数

B定数とは、抵抗-温度特性の任意の2点の温度から求めた抵抗変化の大きさを表す定数をいい、次の式で表されます。

B定数は定数とはいえ実際には一定値ではなく、図3.1.2.1に示すように、高温になるに従ってわずかに大きくなります。 B定数を決定するには、2点の温度Ta、Tbが必要となります。 代表的なものは25℃、85℃でありますが、25℃と50℃や100℃と200℃など用途によって様々であるので、利用の際には注意を要します。 この温度Ta,Tbを明確に表現するためB定数を、Ba/bと表現することとなっております。

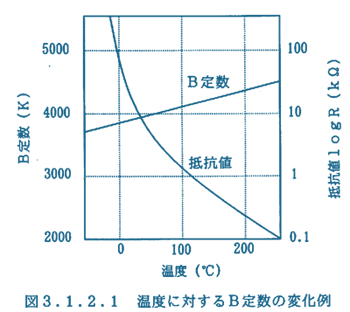
2点の温度Ta、Tbの差が10℃以下では測定温度の誤差によるB定数の誤差が拡大し、一方温度差が100℃を超えると使用する温度付近でのB定数と異なり過ぎることとなります。従って、Ta、Tbの温度差は50℃～100℃が望ましいといえます。
規格値を代表するB定数は、公称B定数と呼ばれ、その推奨許容差はJIS C 2570-1998の中で次のように規定されています。

±0.5%、±1%、±2%、±3%、±5%、±10%、±15%

また、サーミスタの比抵抗とB定数は、材料組成で決まってきます。サーミスタ素子形状が一定であれば、一般的にB定数が大きくなるとゼロ負荷抵抗値が大きくなる傾向にあります。したがって、たとえば同一の素子形状のサーミスタ素子を換えても、B定数とゼロ負荷抵抗値の組み合わせは自由に選択できるわけではありません。

4．ゼロ負荷抵抗温度係数・熱放散定数

ゼロ負荷抵抗温度係数とは、任意の温度Tでの1℃当たりのゼロ負荷抵抗値変化率を表す係数をいい、次の式で表します。

上記の式でわかるように、ゼロ負荷抵抗温度係数（αT）は温度によって大きく変化し、特に低温域では極めて大きくなります。ある温度周辺の温度勾配を直感的に評価する場合には、このゼロ負荷抵抗温度係数（αT）を用いると便利です。

ゼロ負荷抵抗値の温度勾配の評価指数としてはαTとB定数の2つがありますが、 温度勾配の大小だけを比較する場合には、B定数を用いるのが一般的です。

熱放散定数とは、温度安定でサーミスタ素子の温度を自己発熱によって1℃上げるために必要な電力を表す定数をいいます。
サーミスタの消費電力を素子の温度上昇分で除して求め、単位は(mW／℃)で表します。

熱放散定数は、サーミスタの表面積、構造、保護体の材質、環境条件（例えば媒質や媒質の流速など）によって決まります。
熱平衡状態でのサーミスタに供給する電気エネルギーと放熱する熱エネルギーの関係は近似的に次の式で表します。

上記の式は、熱輻射の項を含んでいません。熱放散定数δを一定値と見なせるのは周囲温度が100℃以下の場合であると考えた方がよいこととなります。

5．熱時定数

熱時定数（τ）とは、サーミスタの熱的応答性の度合を表す定数をいいます。
サーミスタの動作はすべて熱現象であるため、必ず時間的遅れが伴います。
サーミスタに電力を負荷し、熱平衡状態からゼロ負荷状態に急変させた時、サーミスタの温度が63.2％変化するのに要する時間が、熱時定数（τ）です。
サーミスタの負荷状態での熱平衡温度Tbをゼロ負荷状態にして、周囲温度Ta（Ta＜Tb）に放置した時のサーミスタの温度変化は、Tbが熱輻射の影響を無視できる100℃以下では、次式の関係が成り立ちます。

すなわち、温度効果（Tb－T）が温度幅（Tb－Ta）の63.2％になる時間がγとなります。このように、サーミスタの周囲温度を急変させたとき、サーミスタの負荷電流をゼロ負荷でない状態からゼロ負荷の状態に急変させた時の熱時定数を、「自己発熱による熱時定数」[thermal time constant by the self-heat dissipation]と呼びます。また、ゼロ負荷の状態で、サーミスタの周囲温度を急変させた時の熱時定数を「周囲温度変化による熱時定数」[thermal time constant by the change of the ambient temperature]と呼びます。サーミスタの構造や保護体によって、この2種類の熱時定数が大きく異なる場合があり、どちらかの熱時定数かを明確にする必要があります。なお、自己発熱による熱時定数には、加熱状態から負荷電流を減じて冷却させる時の冷却時定数と、負荷電流を増加させて冷却状態から過熱させた時の加熱時定数とがあります。

6．カテゴリ温度範囲

カテゴリ温度範囲とは、ゼロ負荷で連続して使用できるサーミスタ素子の温度範囲をいいます。この範囲においてメーカはサーミスタの機能等の品質を保証するものです。したがって、必ずこの温度範囲で使用する必要があります。この「カテゴリ温度範囲」から逸脱した温度で使用した場合、サーミスタ特性の劣化が急速に進む恐れがあり、注意を要します。サーミスタに自己発熱がある場合、実際に使用できる周囲範囲は、カテゴリ上限温度から自己発熱による温度上昇分を差し引いた温度となります。

カテゴリ温度範囲は、一般的にはカテゴリ上限温度とカテゴリ下限温度とで規定されます。低温での使用が主となり高温側は常温であるとき、カテゴリ温度範囲の代わりにカテゴリ下限温度のみが個別仕様書に規定される場合があります。同様に高温での使用が主となり低温側は常温であるとき、カテゴリ上限温度のみが規定される場合があります。

次の表3.4.1に示すように、JIS C 2570-1998の中でカテゴリ温度が規定されています。

7．定格電力

サーミスタに電圧を印加すると、自己発熱していき、周囲の温度に応じた熱平衡温度に到達するが、過大な電力によって熱暴走したり、自己発熱の度合いによっては特性破壊されることもあり、連続して負荷できる電力の上限が定められています。

定格電力とは、個別仕様書で規定された定格周囲温度（一般に25℃）で、連続して負荷できる電力の最大値をいいます。単位はミリワット（mW）で表します。

任意の周囲温度で連続して負荷できる電力の最大値は、最大電力と呼ばれます。周囲温度が定格周囲温度以下の場合、最大電力は定格電力に等しく、周囲温度が定格周囲温度を超える場合、最大電力は電力軽減曲線又はカテゴリ上限温度（θmax）以下において個別規格に規定した温度（θL）で電力を0とした点と定格電力とを結んだ次のような直線から求めることができます。

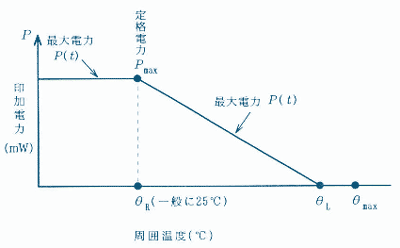
8．図記号及び文字記号の規格

直熱形NTCサーミスタの「図記号」及び「文字記号」は、JIS C 2570-1998で規定されています。

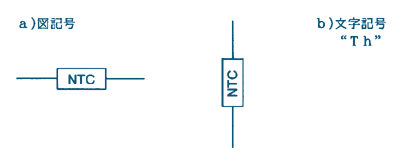
9．温度について

温度とは、我々が温かい冷たいと感じる度合いを数値化したものです。それでは、どのような定義で数値化したかというと、定義の仕方によって3つの温度があります。これらの温度は、ファーレンハイト（Fahrenheit）温度（単位は℉）、セルシウス（Celcius）温度（単位は℃）、熱力学温度（単位はK：ケルビン）と呼ばれています。

ファーレンハイト温度は氷と塩化アンモニウムを混ぜたときの温度と、体温の2点間を96等分したものといわれています。セルシウス温度は氷の氷点と沸点間を100等分したもの、熱力学温度は水の三重点を273.15Kと定義し、この1/273.15をこの温度の単位としています。ファーレンハイト温度（t2）とセルシウス温度（t1）との関係は式5.1及び式5.2で示されます。

この式5.3からセルシウス温度の単位の大きさは、熱力学温度の単位ケルビンに等しいことがわかります。（温度差はケルビン又はセルシウス度で表現する）。

熱力学温度は理想気体を用い、理想状態での圧力の比から求められます。しかし現実には理想気体や理想状態はありえないので、理想に近い条件を整えながら補正を加えて真値を求める努力を行って熱力学温度を求めています。具体的には気体温度計、音速温度計、熱雑音温度計、放射温度計を用いています。

温度という単位も、他の単位（長さや質量）のように国際的に標準化する必要があります。標準化の方法は、定義定点とその定義定点間の補正方法を決めることとなります。
温度の標準で今日用いられているのは、「1990年国際温度目盛」（ITS－90）です。
日本では平成2年10月2日省令として施行されました。

表5. 1にITS－90の定義定点と補間計器を示しました。